Garth Whelan – Page 2 – Aspiring Akmemorph

Biofeedback Smartwatch Update

I’ve been busy recently, with finishing my doctorate and a month long trip. However, I now have a fully wireless biofeedback smartwatch prototype.

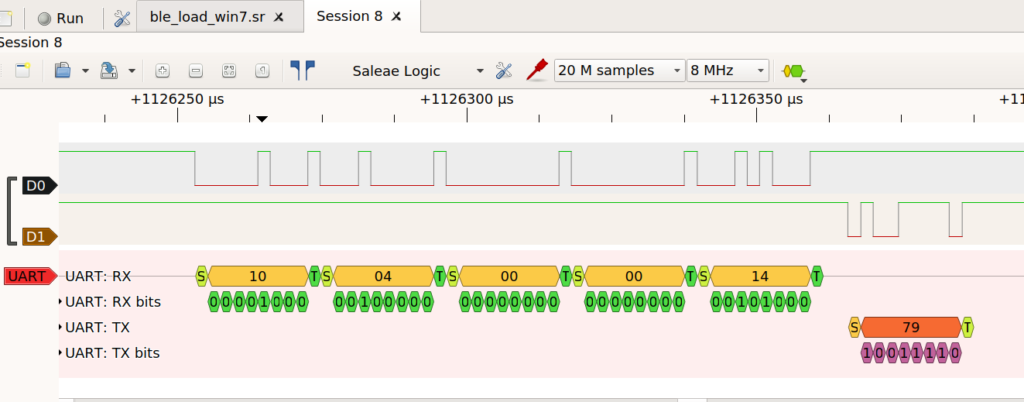
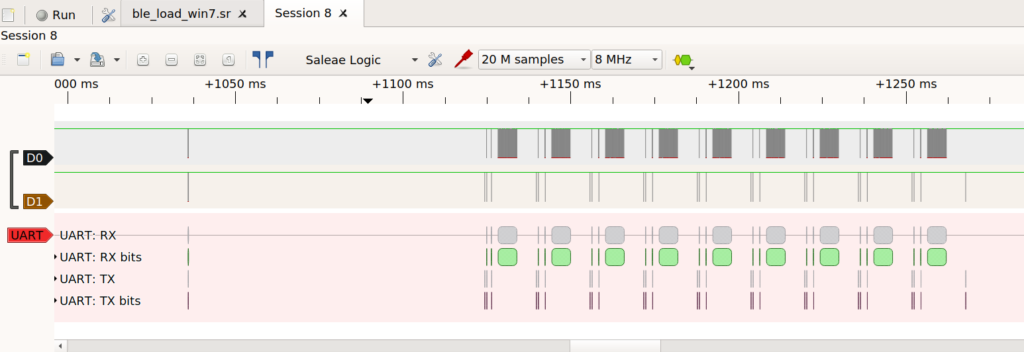
The picture is not fully assembled, but everything works other than the lack of a power switch, usb plug, and IC for charging the Li+ battery on the back. I’ve switched from using a naked nRF52810 IC to a TAIYO YUDEN module, it is more expensive, but I was having a lot of trouble getting antennas to work. The wires to the right are for programming with SWD, and the pair of magnet wires soldered to the board itself are for power so I don’t rundown the battery in testing. To the right of the module are two holes for debugging with UART; it’s been really helpful to use that and the logic analyzer to test things during development.

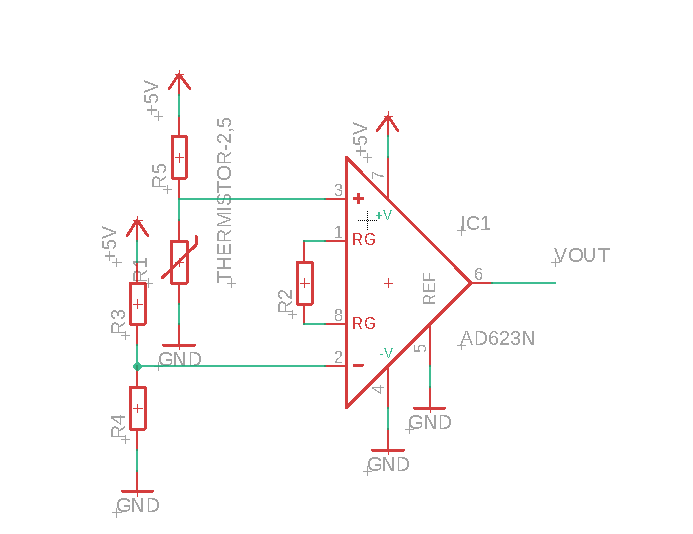
On the finger strap are two electrodes for the GSR voltage bridge, and the MAX30102 SPO2 sensor, which is soldered onto a PCB out of view.

I’m using the following program to activate the ADC and SPO2 sensor and broadcast data over bluetooth. I’m using the nordic UART profile, which contains two characteristics, a read and a write one. I’ve had to learn a lot more about bluetooth than I wanted to for this project.

https://github.com/garthwhelan/NRF-smartwatch/tree/master

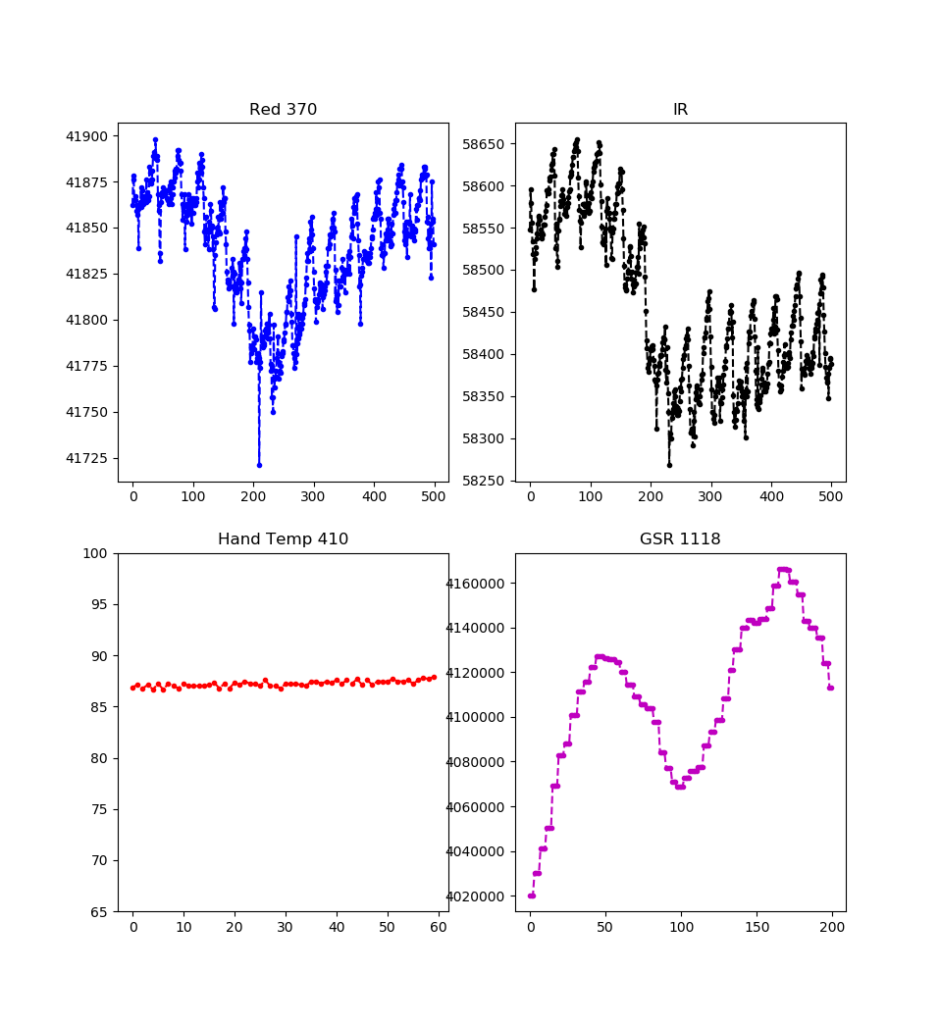
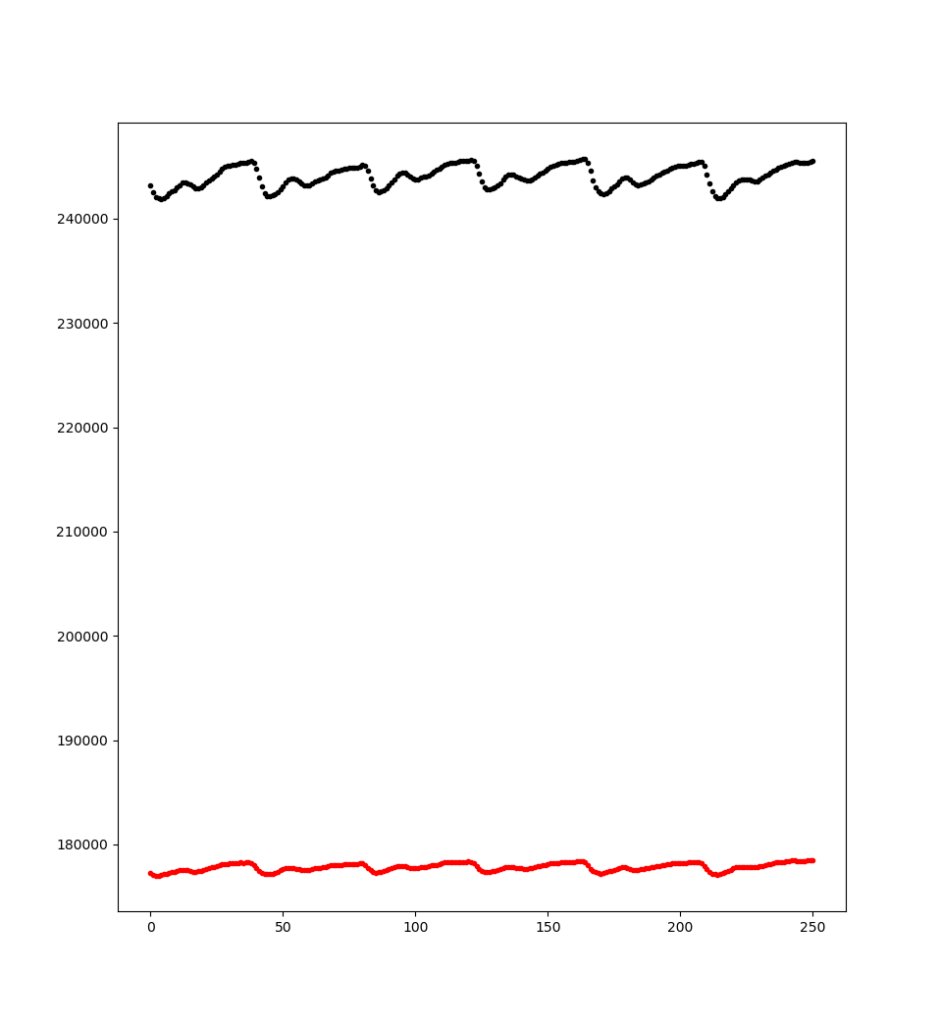
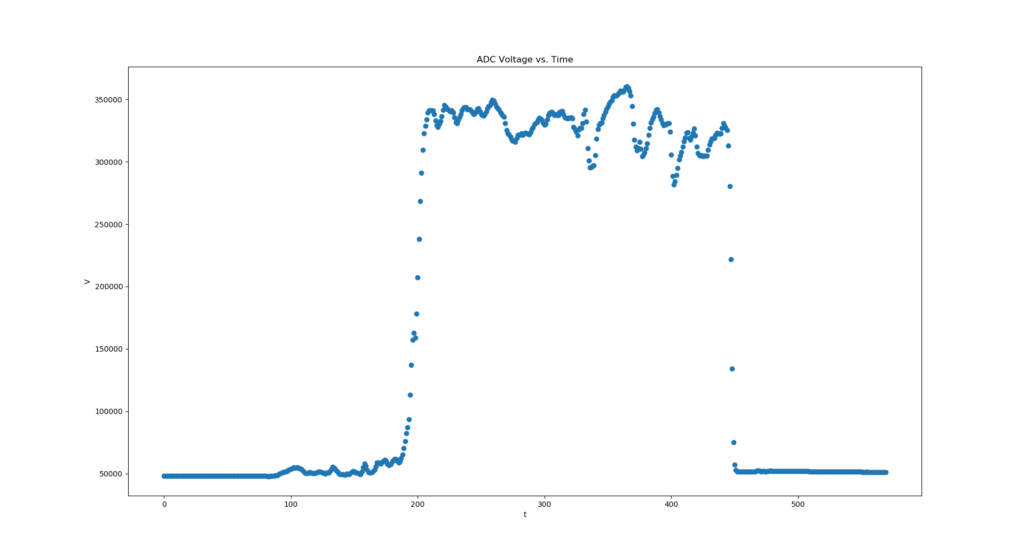
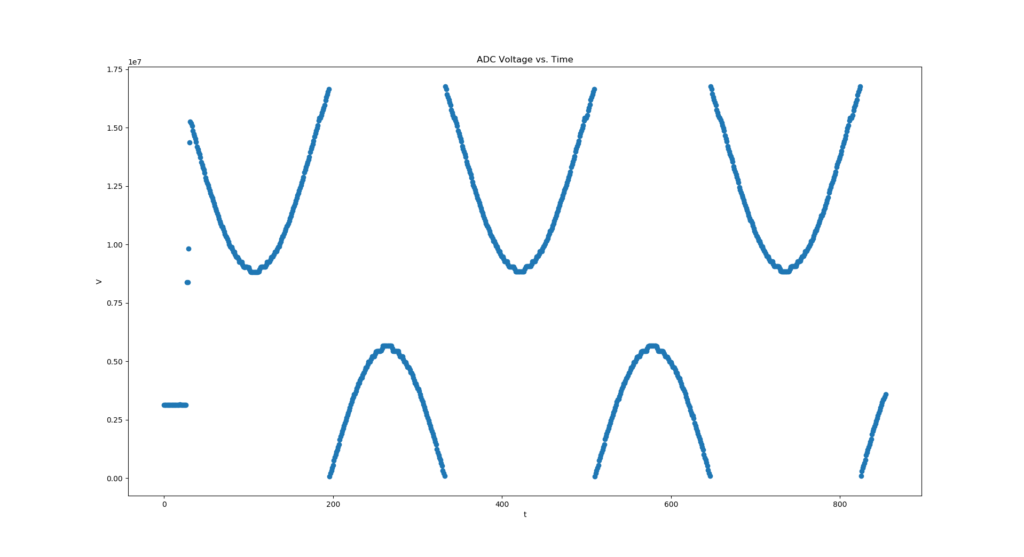
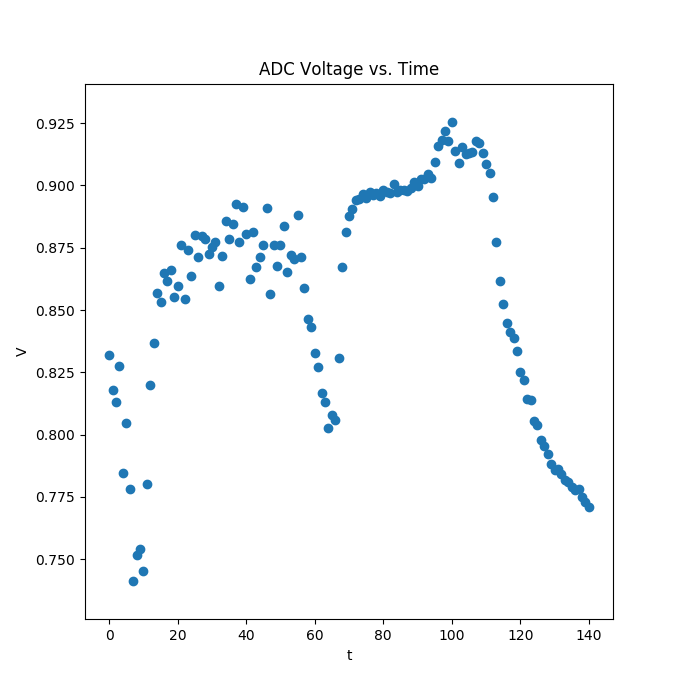
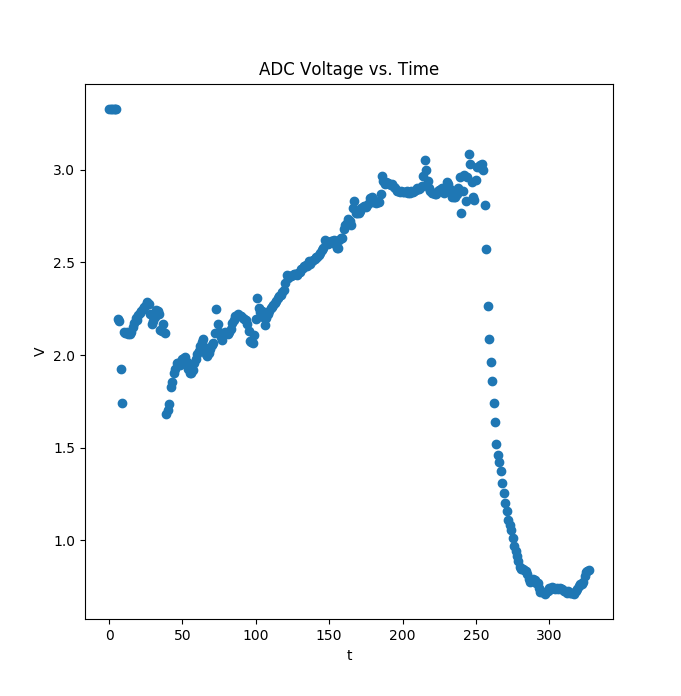
You can see in the above picture I can stream to my laptop, which live plots the data with matplotlib. I’ve had issues with plot update speeds… it sounds like pyqtgraph is a lot faster but not what I want. I’m probably going to try gnuplot if this is still an issue.

On the plotting side, it’s the same as usual, except with the source of data being:


subprocess.Popen("sudo gatttool -i hci0 -t random -b (nrf mac address) --char-write-req -a 0x10 -n 0100 --listen",shell=True,stdout=subprocess.PIPE)

Which writes 1 (0100 reverse endian) to the handle of the characteristic to enable notifications (0x10). Again, there’s a better way to do this with the actual gatt libraries.

In the end I’m pretty happy with everyting. The GSR data is a lot better since switching to a TI adc (ads1246), and the setup is not that encumbering overall. I plan on working on more data analysis for biofeedback (e.g. getting actual SPO2 values, heart rate counters,…) before doing anything with a phone app.

Biofeedback Smartwatch

The PCBs I designed for the Bluetooth biofeedback thing arrived a few days ago. From Oshpark, these were ~10usd total, with free shipping and took ~2 weeks. I’ve never done any QFN soldering (the leads are entirely under the IC) and I didn’t get a solderpaste stencil. Big mistake. Spent a lot of painstaking time with an Exacto knife, sewing needle and tweezers. Also tried using a hot air station for the first time, but a pan on the stove ended up working better.

Small one is meant to be worn on a strap on the finger, the large one is meant to be worn on a strap on the wrist.

SWD pins connected, and it can flash!!!!!!!

Anyway, I got 2 assembled and one of them works with my st-link and openocd. Unfortunately I lost all of my rf inductors during assembly (also the only parts I lost), so I can’t test the bluetooth. I’m using the nRF52810, have downloaded the SDK kit from https://www.nordicsemi.com/Software-and-Tools/Software/nRF5-SDK/Download#infotabs, and can get the examples to compile with the compiler from https://developer.arm.com/tools-and-software/open-source-software/developer-tools/gnu-toolchain/gnu-rm. I’m mentioning where I got the compiler because I spent a few hours trying to get the gentoo package crossdev working before just downloading binaries.

openocd -f ~/openocd/tcl/interface/stlink.cfg -f ~/openocd/tcl/target/nrf52.cfg -c “program nrf52810_xxaa.bin verify reset exit”

Because it will take time anyway for new inductors to arrive, I did a redesign and ordered more boards. I hope to actually be able to wear the next generation around. I’ll put in some filler posts on computing before then.

Sorting LaTeX references

I don’t use .bib files and just populate bibliographies like:


\begin{thebibliography}{99}



\bibitem{Romanelli1989}

  F.~Romanelli, Phys. Fluids B \textbf{1}, 1018 (1989).



%.... (other citations)

One issue is that this can be out of order compared to the order of /cite{} in the text. The following python script goes through the citations in the text and prints the appropriately ordered bibliography. Replacing the bibliography must be done by hand, but it’s safer that way.


f=open("article.tex","rb")



cites=&#91;]

A=f.tell()



for line in f.readlines():

  while(True):

    a=line.find(r"\cite{")

    if(a==-1):

      break

    else:

      line=line&#91;a+5:]

      b=line.find("}")

      blah=line&#91;1:b]

      if(blah!=""):

        B=blah.split(",")

        for e in B:

          if e not in cites:

            cites.append(e)

      line=line&#91;b:]



refs=&#91;]



f.seek(A)

last_line=""

for line in f.readlines():

  if(last_line&#91;:5]==r"\bibi"):

    refs.append((last_line,line))

  last_line=line



for i in cites:

  for j in refs:

    end=j&#91;0].find("}")                                                                                                                                        

    if(i==j&#91;0]&#91;9:end]):

      print j&#91;0]&#91;:-1]

      print j&#91;1]

      continue

BlueNRG2

Very much in the spirit of the 90-90 rule, this took much longer than I assumed.

So my goal is to put the galvinic skin response, hand temperature and SPO2 sensors onto a ring connected to a bluetooth ‘watch’, and have some phone app which can stream the data. To play around with a microcontroller which has bluetooth, I got the STEVAL-IDB008V2 dev board, which has a BlueNRG2 chip. Because I’ve only played with the Nucleos so far, I was overoptimistic about linux compatibility. On the plus side, my setup for development has gotten much more comfortable-I’m back to using emacs and makefiles, and I’ve learned how to use st-util to flash and debug and I’ve also gotten my first experience using logic analyzers with sigrok and pulseview.

The issue which held me up was actually getting the programs onto the chip. While the dev board has a JTAG header, the default application disables those pins so it cannot be programmed in that way. The alternative is to flash it with the UART bootloader, which requires the chip be booted into a specific mode and a different pair of pins.This board has a USB, but unlike the nucleos, it is not connected to a ST-Link. All of the software for flashing the chip was windows-only, and I had a lot of trouble getting that working.

Anyway, after much toil I managed to work out a way to reliably flash the chip using the windows software on a VM, but at this point I had already mostly written a bootloader using a nucleo as an intermediary. A warning on the very slim odds a reader will be stuck on the bootloader like I was. As far as I can tell, the bootloader will respond with a positive acknowledge even to invalid addresses, only to fail when receiving the data to flash. To work the last bugs out of the bootloader I was working on, I compared the output of the logic analyzer for each of them flashing the chip with the same data. This revealed that the address bytes I was using were off allowing me to fix the program.

~10usd logic analyzer that’s already worth it

Address bytes and acknowledge in Pulseview

Full writing in pulseview. First is the erase command, followed by blocks of 256 bytes.

Photoplethysmogram 3

I’ve gotten all of the sensors working at once now. One of the changes is that I’m now using a ’24’ bit differential external ADC. I’m using the NAU7802, which communicates with I2C and runs at a very slow 10-320 SPS. This is plenty fast and seems to be high enough resolution to measure GSR without any external amplifier. The ADC also has an internal PGA which hasn’t been nessesary so far.

The spikes in graphs below for red and IR correspond to heart rate.

I’m currently using the MAX30102’s temperature sensor (which is meant for the LEDs) to measure finger temp. I will have to decide whether this is good enough.

I made several attempts dead-bug soldering the NAU7802. What worked best was to glue to face down on a peice of cardstock and then just solder to the prongs from there.

Photoplethysmogram 2

The MAX30102 arrived and I spent some time. I’ve also gotten metal disks and will try to make rings with polymer clay to hold the electrodes for GSR on better. As such I’m busy and this will be brief.

After reading through the datasheets, I wrote something to set registers for SpO2 measurements (IR and red LEDs active, there’s a heart rate mode with only one), and after having bad luck with guessing appropriate settings, eventually found all the recommended settings in the application notes for the demonstration board.

I had a bit of difficulty getting data from it, if just because it’s smart. There’s a 32 sample FIFO circular buffer for the data, which is accessed by repeated reading a single byte register. The read and write pointers are accessible but unnessesary for this, as they both automatically increment. Samples are 2 24 bit numbers (IR and red channel). As is, the program I’m using to read data sets an interrupt enable flag on the MAX30102 to check it for available data and then checks it repeatedly. There is also an almost full interrupt, and I spent some time getting the MAX30102 to trigger the nucleo, but I’m still having trouble reading multiple samples from the ADC.

See https://github.com/garthwhelan/Nucleo-MAX30102, which I will hopefully have enough time to make nice because I plan to use this with hand tempurature and GSR for biofeedback.

Anyway, in the end I got a reasonable trace for reflectance values.

Photoplethysmogram part 1

In which I trudge through some simple tests and realize it helps to read a bit before starting things. Today I tried to make a very very simple photoplethysmogram (light-enlargment-gram). Flesh is relatively transparent to red and infrared light, and that changes with the amounts of blood in one’s tissue. This can be used to measure heart rate. The light absorption of hemoglobin changes depending on whether it is attached to oxygen or not. This can be used to measure heart rate too, as well as oxygen saturation (pulse oximetry).

https://en.wikipedia.org/wiki/Photoplethysmogram (PPG)

https://en.wikipedia.org/wiki/Pulse_oximetry

A nice combination of sensors for a wearable watch+ring would be PPG, perifereal temperature and galvinic skin response. I spent a couple of hours trying to get a basic PPG with some IR LEDs and photodiodes. Unfortunately I charged ahead without reading anything and now realize that PPGs are done differently from what I had assumed. Basically, I was just trying to measure IR light reflected (diffusely) by tissue over time.

I bought some 940 nm IR LEDs and photodiodes and made a photointerrupter as a test (read: pointed them at each other and looked at voltages as I put my hand between them). I also played with them as a distance sensor by reflecting the IR off of objects. This was neat.

IR led (which has a neat blue glow on camera) and photodiode, with voltage measured by the oscilloscope. I tried multiple distances and orientations.

Unfortunately there was no obvious change in reflected IR during a heartbeat when they were pointed into my wrist. I moved them much closer, which caused the diode to always be saturated. I then tried it with a shield around the IR led made of tin foil, securing them together with hot glue. The diode was always saturated in this case as well.

I then tried seperating them with a peice of cardboard. This worked and generated a very small signal fluctuating with my heart beat when it was pressed against flesh. I’m not confident that this was PPG as opposed to just changes in distance and pressure.

For PPG beyond wikipedia:

https://www.researchgate.net/publication/224765089_Pulse_Oximeter_Waveform_Photoelectric_Plethysmography

Takeways:

For PPG, only 940nm is displayed (as above).
Finger tips are the best position (assuming transmission here).
Strain gauges have been used to measure heart rate.

For pulse oximetry:

https://www.sciencedirect.com/science/article/pii/S2405959516301205#br000015

Oximetry is done with a pair of LEDs, a red (660 nm) and an IR one (940nm). Hemoglobin with oxygen absorbs more infrared (NOTE: the paper has an error here “more infrared light (660 nm wavelength) and lesser red light (940 nm wavelength) than Hb.” reverses the frequencies compared to the colors).

Stolen from http://www.dnatechindia.com/basic-working-pulse-oximeter-sensor.html

The ratio of the varying to constant intensities of each LED color is calculated, and the ratio of the two ratios is compared to an empirical fitting to give the saturated O2 levels. Measuring this accurately by reflection is hard, the paper reads as a failure (“presents challenges”), but heart rate is easier than oxygen saturation.

Hand dynamometer-part 2

I carved handles out of wood and mounted the strain sensors in it.

Gripping it as hard as I can. Was interesting to see grip strength fail and then increase again when I redoubled my efforts.

Seems to be a working, if low quality dynamometer. If I was to redo this I would build more around the grip and possible use different strain sensors. I might measure the effects of irraditation (tensing other muscles in this context) on grip strength later.

HX711 – Dynamometer part 1

Grip strength can be used as a measure of overtraining.

There are ADC + strain gauge meters on ebay for hobby bodyweight scales (HX711) that should be good for measuring up to around 200kgs. I ordered one and plan to put the gauges between a pair of half cylinders of wood to measure grip strength.

The HX711 can communicate with microcontrollers with a 2 wire interface like I2C. I’ve gotten this working with the Nucleo and tested it by having the Nucleo output a sin wave and reading the voltage that the HX711 measured.

project stuff here, remember that all the Nucleo stuff is compiled using the mbed compiler

Voltage measured by the HX711. Output is in two’s complement, which is why the sin wave is split between top and bottom. You can see the quantization in the DACs output because there’s a minimum 64 fold amplification for the HX711. This means that even a tiny voltage swing will saturate the output.

Galvinic Skin Response and Hand Temperature

Two biofeedback sensors I can probably get working faster than the EEG are hand temperature and galvinic skin response. Hand temperature biofeedback is mostly used to train relaxation. Adrenaline restricts bloodflow to the skin and hands, so by training yourself to warm your hands you can learn to reduce adrenaline levels. Galvinic skin response is similar. People sweat more when nervous, filling sweat ducts with sweat. This is most pronounced on the hands and feet. Sweating reduces skin resistance by providing a conductive channel into the skin. This effect happens in seconds, and is used in polygraphs to detect lies.

For the most part, the resistance inside the body is low enough not to matter when measuring galvinic skin response. The simplest way to measure skin resistance is to put a current through two electrodes in contact with the skin and measure the voltage difference. This is usually done with electrodes on the index and ring fingers.

(For much more detail on measuring galvinic skin response, see Electrodermal Activity by Wolfram Boucsein)

While high temperature measurements usually use thermocouples, the easiest way to measure hand temperature is by using thermistors. The thermistors linked go between about 80k-100k Ohms around 70-100F. They are incredibly small, which gives them really fast response times and makes it easy to keep them around skin temperature.

For measuring each of these resistances, I constructed voltage bridges with instrumentation amplifiers to increase the voltage range. I then used the integrated ADCs in the Nucleo microcontroller I have to measure the voltage.

Set up the voltage bridge with R3/R4 to be a bit below the lowest voltage between R1/R5. Select gain resistor so that Vout is below 3.3V when R1 at its highest. This setup can be used with both GSR and hand temp, but will require different resistors. GSR would probably benefit with variable resistors to set gain and comparison voltage.

See https://github.com/garthwhelan/Nucleo-ADC/tree/master for example which reads the ADC 10 times a second and communicates it to a python program on a host which plots the output.

Plot of voltage measured for thermistor as I grabbed an icepack at t=50 and t=110.

Voltage for skin resistance, again grabbing an icepack at T=220

Like the EEG project, actually having a wearable probe is difficult. For GSR, I used the following copper coils:

I also tried mounting the thermistors in sections of pipe which I could use as GSR electrodes. While it looks neat, I think it will require rings which fit better.